|
On considère le tir
d'un boulet de canon selon le schéma suivant. Le tir est
effectué d'une tranchée et l'altitude du boulet
au temps t=0 s est donc nulle .
Mboulet
= 2 kg , α
= 40° , V0 = 80 m.s-1
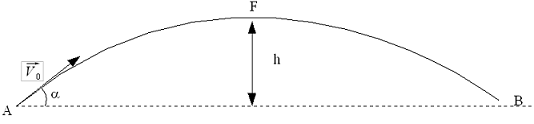
1- Quelle est la seule force qui
s'exerce sur le boulet si l'on
considère les frottements comme étant
négligeables
. (nom et caractéristiques)
2- Comment évolue précisément
la
vitesse au cours du mouvement ?
3- Quelle
est la valeur de la
vitesse au point le plus haut de la trajectoire ?
Quel est le principe
appliqué ? (Le nommer et l'énoncer)
4- Exprimer l'énergie
mécanique au point A .
5- Calculer l'énergie
potentielle au point F .
6 – Exprimer
littéralement la hauteur maximale atteinte
en fonction de la vitesse au point A .
7- Calculer h .
8- Quelle sera la vitesse du boulet au
point B ? Quel est la
principe appliqué ?
Correction
Exercice
II :
Dans
un parc d'attraction , on peut trouver des manèges
appelés montagnes russes . On considère une
portion de ce manège .
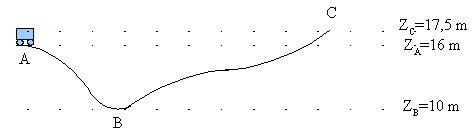
La
vitesse du chariot en A est VA = 6 m.s-1
.
1- En
utilisant la loi de conservation de l'énergie
mécanique , exprimer en fonction de ZA, ZB
ou ZC les vitesses
aux points B et C . Calculer ces vitesses .
2-
Après le point C , le manège continue son
ascension . Exprimer ZD la hauteur maximum
atteinte en fonction de ZA
et de VA . Calculer cette hauteur .
Réponses
Exercice III :
Mathieu essaye de vérifier la conservation de l'énergie mécanique sur
une balançoire bien graissée (pour rendre les frottements négligeables)
. Il filme donc un de ces camarades pour pouvoir étudier le mouvement .(vidéo)
En utilisant le logiciel dynamic , déterminer la
vitesse instantanée lors du passage par la position
d'équilibre . ( on donne : La
distance entre le sol et le repère blanc vaut 1,0 m.
L'intervalle
de temps entre 2 images successives vaut 40 ms )
En
appliquant la loi de conservation de l'énergie mécanique (frottements
négligeables) déterminer la hauteur relative maximum que peut atteindre
la personne sur la balançoire . Vérifier alors sur la vidéo .
(attention , la position du centre de masse de la personne qui est
approximativement au milieu du ventre ne se trouve pas à z = 0 m
lorsque la balançoire est verticale)
|