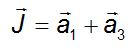a_3Maxi = 28,52 mm

a_3mini = 28,48 mm

J = a₃ – a₁

J_Maxi = a_3Maxi – a_1mini

J_mini = a_3mini – a_1Maxi

IT _J = IT a₁ + IT a₃

Condition fonctionnelle

Le coussinet 1 étant monté serré dans la bielle 2, il faut qu'après serrage de l'écrou supérieur, il y est un jeu J entre la rondelle  et la face supérieure du coussinet. La rondelle doit donc être en contact avec la face de l'épaulement de l'arbre 3.

Afin que le déplacement axial de la bielle ne soit pas trop important, ce jeu est fixé (par le concepteur) à 0,8mm au maximum avec un minimum de 0,2mm.

Donnée:       Le coussinet est un élément standard. Sa longueur est de 28mm avec une tolérance de ±10% de la longueur (donnée fourni par le fabricant).

Problème:    Déterminer la longueur de l'épaulement pour respecter les conditions fonctionnelles.

Voici quelques règles simples qui s'appliquent à la construction des chaînes de cotes. La chaîne de cotes débute à l'origine du vecteur condition et se termine à son extrémité, de sorte que : 

1. Chaque cote de la chaîne, commence et se termine sur la même pièce. (Le problème initial est de coter les différentes pièces du mécanisme)
2. Il ne peut y avoir qu'une seule cote par pièce dans une même chaîne de cotes. La chaîne de cotes doit être la plus courte possible, afin de faire intervenir le moins de cotes possible. Si deux cotes de la chaîne appartiennent à la même pièce, c'est qu'il existe une chaîne de cotes encore plus courte réalisant le même vecteur condition,
3. Le passage d'une cote de la chaîne à la suivante se fait par la surface d'appui entre les deux pièces cotées. En effet, la fermeture vectorielle exprimée plus haut n'a de sens que si les origines des différents vecteurs correspondent aux extrémités du vecteur précédent,
4. La somme des intervalles de tolérance des cotes intervenant dans une chaîne de cotes est égale à l'intervalle de tolérance de la cote condition. Cette propriété impose de choisir pour les cotes conditions des IT les plus larges possibles, afin de réduire le coût des pièces entrant dans la constitution de la chaîne.

IT _{Cote Condition} =  Σ IT_{Cotes Composantes}